[NLP] 오차역전파로 간단한 mnist 학습 진행 (모든 계층을 직접 코딩해보자)

 

 

 

이전 포스팅에 이어서 활성화 함수 계층 구현부터 배워보겠다.

• 이전 포스팅 > https://dokylee.tistory.com/36

[NLP] 오차역전파법 역전파 backpropagation

 

 

 

이번 포스팅에서는 계산 그래프를 신경망에 적용해보자.

 

 

 

활성화 함수 계층 구현하기

---

1. ReLU 계층 구현

 

활성화 함수로 사용되는 ReLU의 수식은 다음과 같다.

 

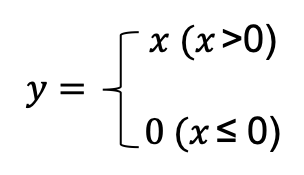
그림 1

[그림 1]에서 x에 대한 y의 미분은 [그림 2]처럼 구한다.

 

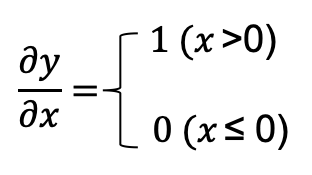
그림 2

 

[그림 2]에서와 같이 순전파 때의 입력인 x가 0보다 크면 역전파는 상류의 값을 그대로 하류로 흘린다.

 

반면, 순전파 때 x가 0 이하면 역전파 때는 하류로 신호를 보내지 않는다(0을 보낸다).

 

계산 그래프로는 [그림 3]처럼 그릴 수 있다.

 

그림 3

 

이제 구현해보자.

 

 

 

 

 

class Relu:
    def __init__(self):
        self.mask = None
        
    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0
        
        return out
    
    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        
        return dx

mask는 True/False로 구성된 넘파이 배열로, 순전파의 입력인 x의 원소 값이 0 이하인 인덱스는 True, 그 외(0보다 큰 원소)는 False로 유지한다.

 

순전파 때의 입력 값이 0 이하면 역전파 때의 값은 0이 돼야 한다. 

 

그래서 역전파 때는 순전파 때 만들어둔 mask를 써서 mask의 원소가 True인 곳에는 상류에서 전파된 dout을 0으로 설정한다.

 

 

 

2. Sigmoid 계층 구현

 

시그모이드 함수 수식은 다음과 같다.

 

그림 4

이를 계산 그래프로 그리면 [그림 5]처럼 된다.

 

그림 5

 

 

[그림 5]와 같이 [그림 4]의 계산은 국소적 계산의 전파로 이뤄진다.

 

이제 [그림 5]의 역전파를 알아볼 차례다.

 

단계별로 보겠다.

 

 

1단계

'/' 노드, 즉 y=1/x 을 미분하면 다음 식이 된다.

 

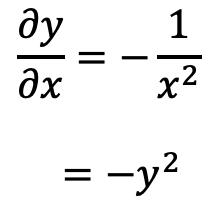
그림 6

 

[그림 6]에 따르면 역전파 때는 상류에서 흘러온 값에 -y^2 (순전파의 출력을 제곱한 후 마이너스를 붙인 값)을 곱해서 하류로 전달한다.

 

계산 그래프에서는 다음과 같다.

 

그림 7

 

 

 

 

2단계

'+' 노드는 상류의 값을 여과 없이 하류로 내보내는 게 전부다.

 

계산 그래프에서는 다음과 같다.

 

그림 8

 

 

 

3단계

'exp' 노드는 y=exp(x) 연산을 수행하며, 그 미분은 다음과 같다.

 

그림 9

계산 그래프에서는 상류의 값에 순자파 때의 출력 (이 예에서는 exp(-x))을 곱해 하류로 전파한다.

 

그림 10

 

 

 

 

4단계

'x' 노드는 순전파 때의 값을 '서로 바꿔' 곱한다. 이 예에서는 -1을 곱하면 된다.

 

그림 11

 

역전파의 최종 출력인 ∂L/∂y y^(2 ) exp⁡(-x)를 순전파의 입력 x와 출력 y만으로 계산할 수 있다는 것을 이용하여

 

[그림 11]의 계산 그래프의 중간 과정을 모두 묶어 [그림 12]처럼 단순한 'sigmoid' 노드 하나로 대체할 수 있다.

 

그림 12

또한 ∂L/∂y y^(2 ) exp⁡(-x) 는 다음처럼 정리해서 쓸 수 있다.

그림 13

이처럼 sigmoid 계층의 역전파는 순전파의 출력(y)만으로 계산할 수 있다.

 

그림 14

 

이제 구현해보자.

class Sigmoid:
    def __init__(self):
        self.out = None
        
    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        
        return out
    
    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        
        return dx

 

이 구현에서는 순전파의 출력을 인스턴스 변수 out에 보관했다가, 역전파 계산 때 그 값을 사용한다.

 

 

 

 

 

Affine 계층 구현하기

---

신경망의 순전파에서는 가중치 신호의 총합을 계산하기 때문에 행렬의 곱 (넘파이에서는 np.dot())을 사용했었다.

 

신경망의 순전파 때 수행하는 행렬의 곱은 기하학에서는 어파인 변화(affine transformation)이라고 한다. 

 

어파인 변환을 수행하는 처리를 'Affine 계층'이라는 이름으로 구현하겠다.

 

 

앞에서 수행한 계산 (행렬의 곱과 편향의 합)을 계산 그래프로 그려보자. [그림 15]처럼 그려진다.

 

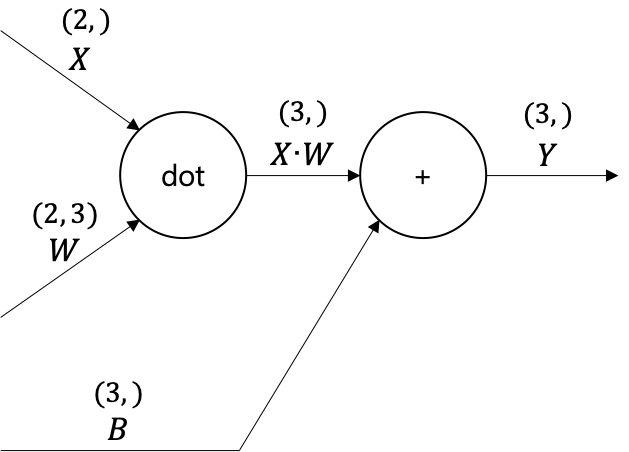
그림 15

 

[그림 15]는 X, W, B가 행렬(다차원 배열)이라는 점에 주의하자.

 

지금까지의 계산 그래프는 노드 사이에 '스칼라값'이 흘렀는 데 반해, 이 예에서는 '행렬'이 흐르고 있는 것이다.

 

[그림 15]의 역전파인 행렬을 사용한 역전파도 행렬의 원소마다 전개해보면 스칼라값을 사용한 지금까지의 계산 그래프와 같은 순서로 생각 할 수 있다.

 

실제로 전개해보면 다음 식이 도출된다.

 

그림 16

[그림 16]을 바탕으로 계산 그래프의 역전파를 구해보자.

 

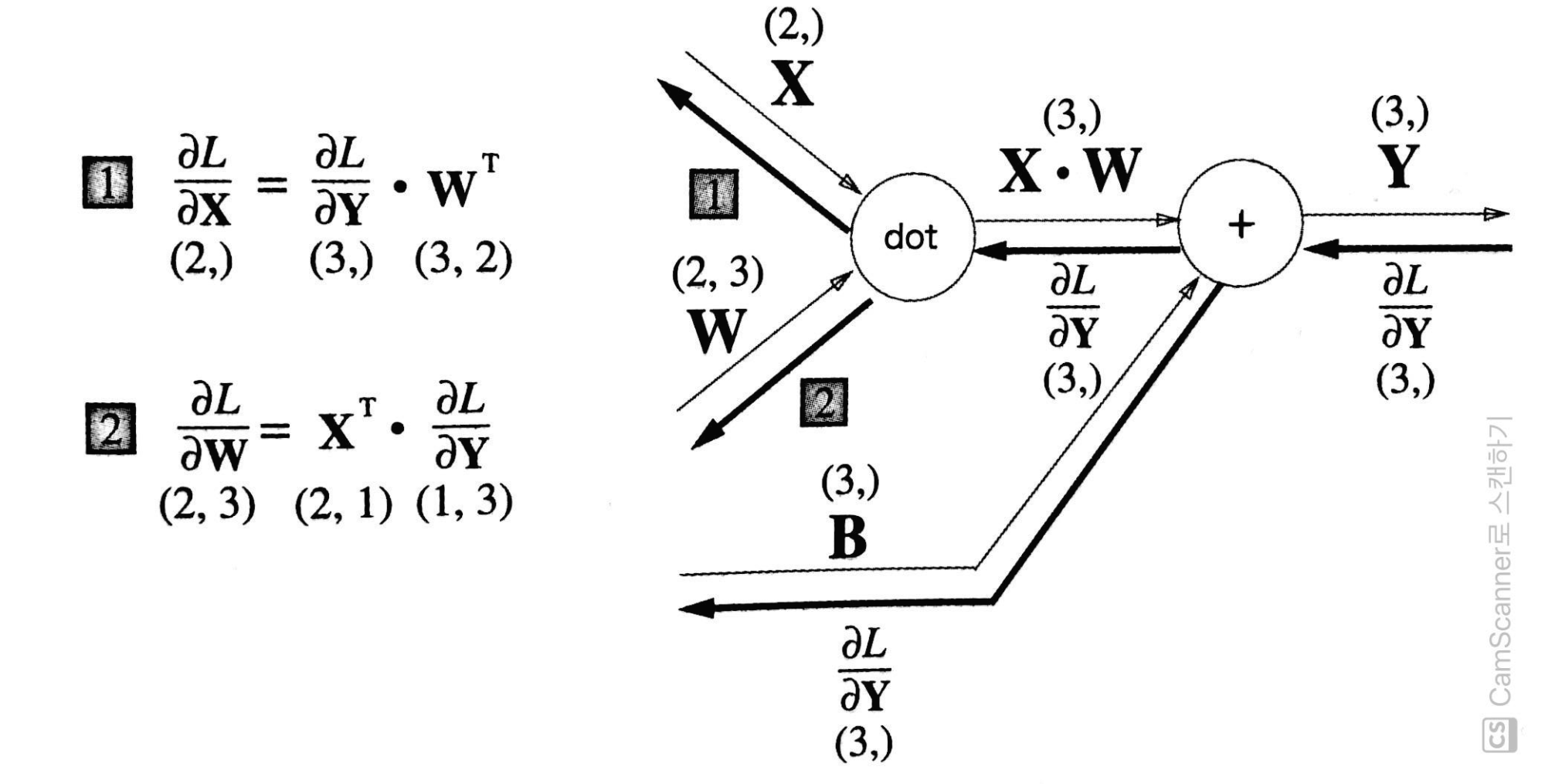
그림 17

[그림 17]의 계산 그래프에서는 각 변수의 형상에 주의해서 살펴보자.

 

특히 X와 ∂L/∂X은 같은 형상이고, W와 ∂L/∂W도 같은 형상이라는 것을 기억하자.

 

X와 ∂L/∂X의 형상이 같다는 것은 다음 식을 보면 명확하다.

 

그림 18

 

행렬의 곱에서는 대응하는 차원의 원소 수를 일치시켜야 하는데, 이를 위해서는 [그림 16]을 동원해야 할 수도 있기 때문이다.

 

예를 들어 ∂L/∂Y의 형상이 (3,)이고 W의 형상이 (2, 3)일 때, ∂L/∂X의 형상이 (2,)가 되는 ∂L/∂Y과 W의 곱을 생각해보자(그림 19).

 

그러면 자연히 [그림 16]이 유도될 것이다.

 

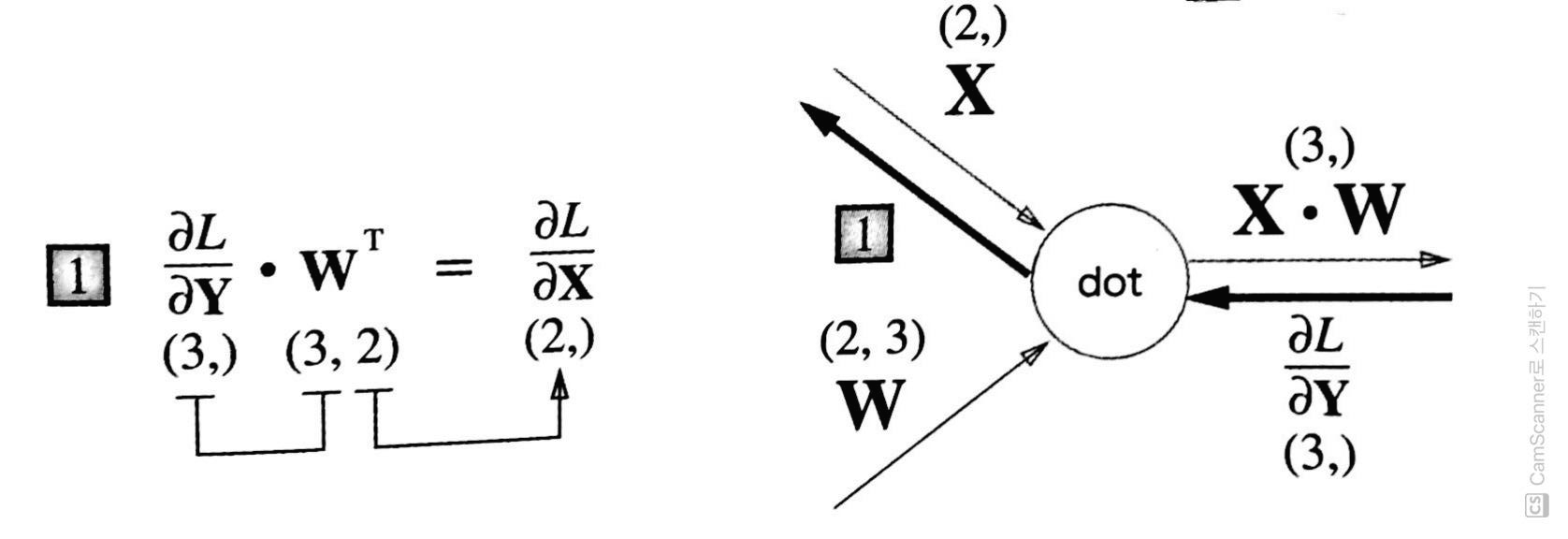
그림 19

==> 행렬 곱('dot'의 노드)의 역전파는 행렬의 대응하는 차원의 원소 수가 일치하도록 곱을 조립하여 구할 수 있다.

 

 

 

 

 

배치용 Affine 계층

---

이번에는 데이터 N개를 묶어 순전파하는 경우, 즉 배치용 Affine 계층을 생각해보겠다(그림 20).

 

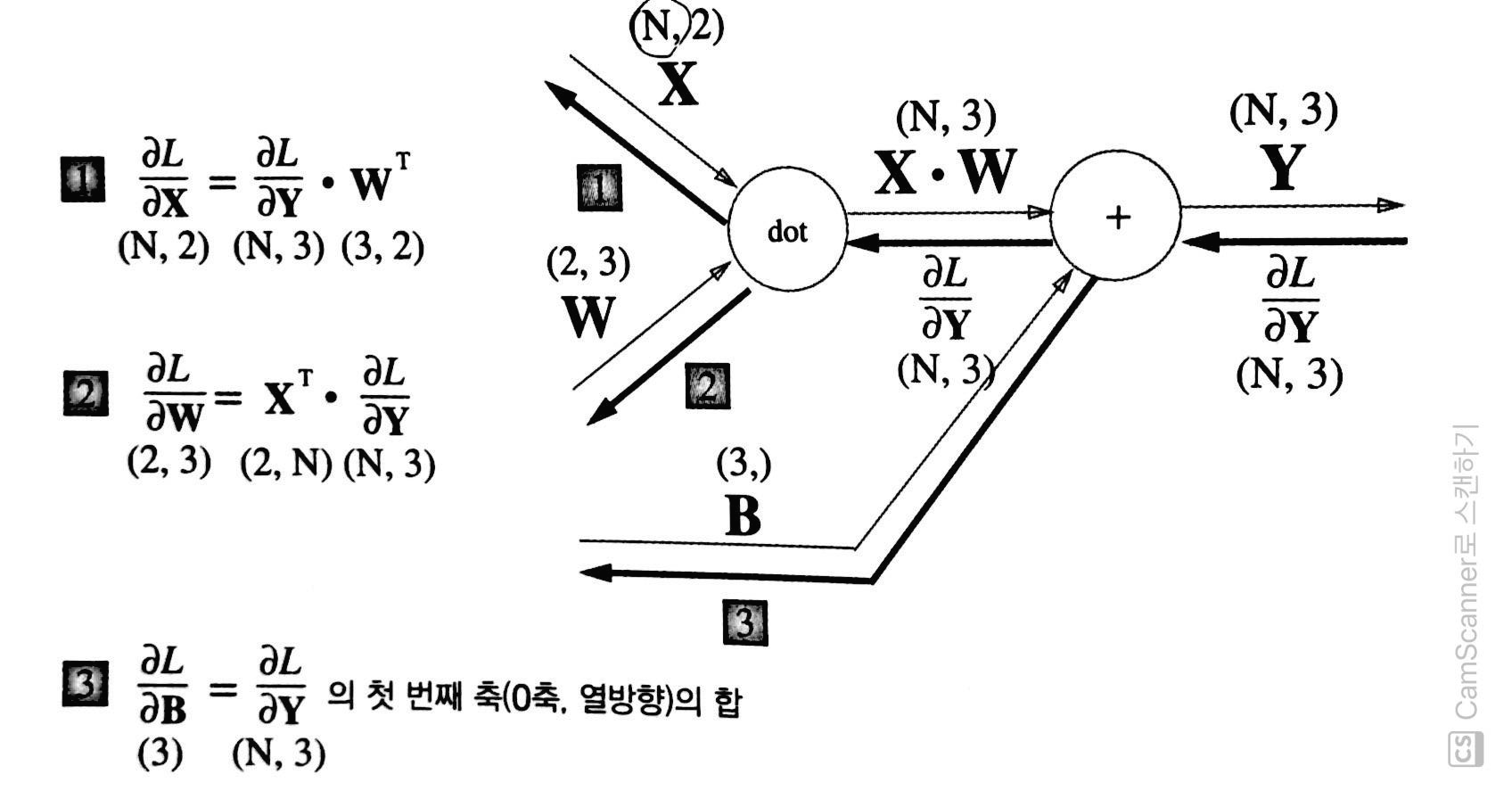
그림 20

 

기존과 다른 부분은 입력인 X의 형상이 (N, 2)가 된 것뿐이다. 

 

편향을 더할 때도 주의해야 한다. 순전파 때의 편향 덧셈은 X·W에 대한 편향이 각 데이터에 더해진다.

 

직접 Affine 구현을 해보자.

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None
        
    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        
        return out
    
    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        
        return dx

 

 

 

 

Softmax-with-Loss 계층

---

softmax 함수는 입력 값을 정규화하여 출력한다.

 

예를 들어 손글씨 숫자 인식에서의 Softmax 계층의 출력은 [그림 21]처럼 된다.

 

그림 21

 

==> 입력 이미지가 Affine 계층과 ReLU 계층을 통과하며 변환되고, 마지막 Softmax 계층에 의해서 10개의 입력이 정규화된다. 이 그림에서는 숫자 '0'의 점수는 5.3이며, 이것이 Softmax 계층에 의해서 0.008(0.8%)로 변환된다. 또, '2'의 점수는 10.1에서 0.991(99.1%)로 변환된다.

 

 

[그림 21]과 같이 Softmax 계층은 입력 값을 정규화(출력의 합이 1이 되도록 변형)하여 출력한다.

 

또한, 손글씨 숫자는 가짓수가 10개(10클래스 분류)이므로 Softmax 계층의 입력은 10개가 된다.

 

 

** 신경망 작업에서 학습에서는 Softmax 계층이 필요하지만, 추론에서는 Softmax 계층 없이 Affine 계층의 출력을 인식 결과로 이용한다.

 

 

소프트맥스 계층을 구현할 것인데, 손실 함수인 교차 엔트로피 오차도 포함하여 'Softmax-with-Loss 계층'이라는 이름으로 구현하겠다.

 

먼저, Softmax-with-Loss 계층의 계산 그래프를 살펴보자.

 

그림 22

 

보다시피 Softmax-with-Loss 계층은 다소 복잡하다. 그러므로 여기서는 결과만 제시하겠다.

 

[그림 22]의 계산 그래프는 [그림 23]처럼 간소화할 수 있다.

 

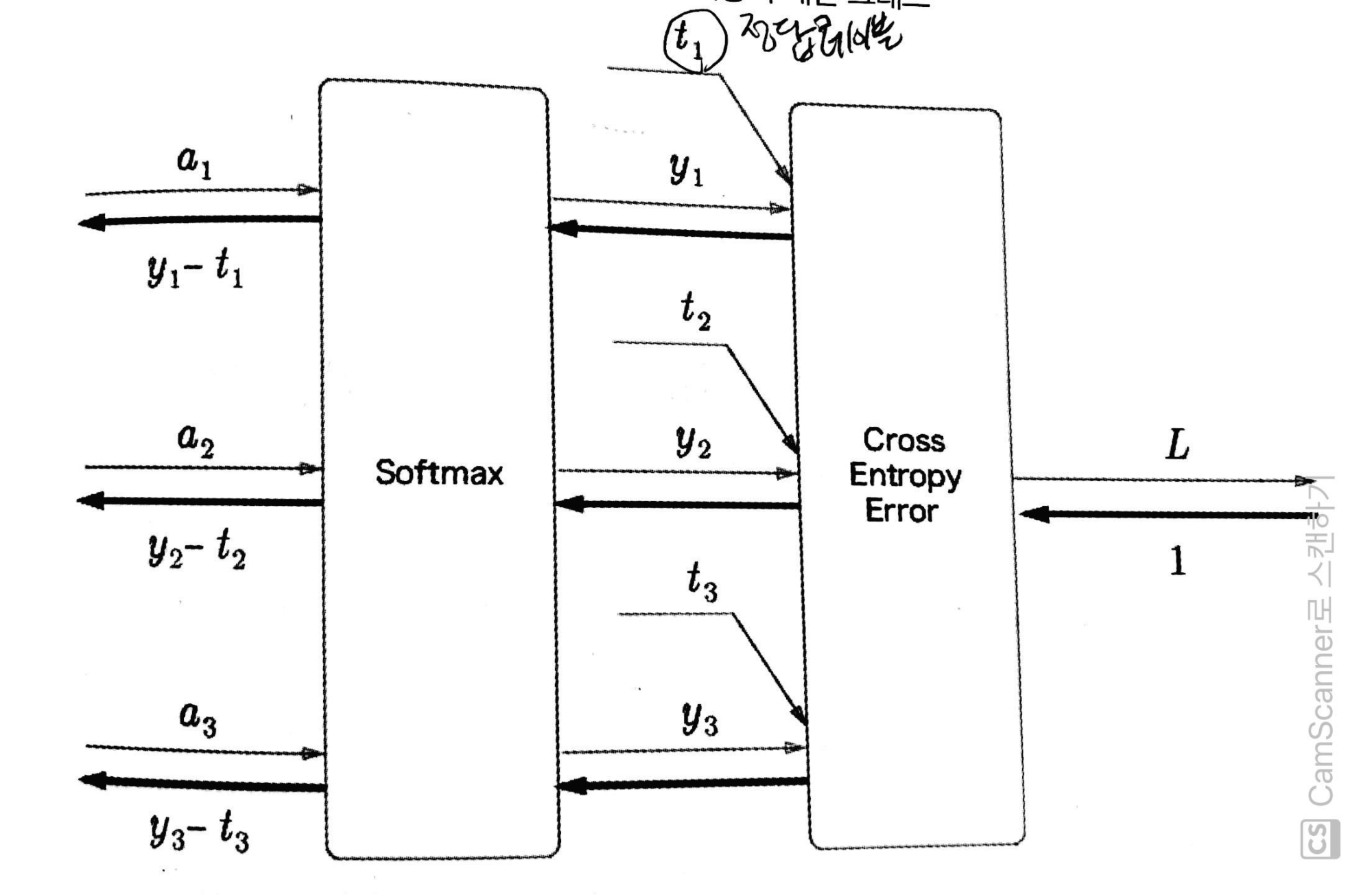
그림 23

 

[그림 23]과 같이 Softmax 계층은 입력 (a1, a2, a3)를 정규화하여 (y1, y2, y3)를 출력한다.

 

Cross Entropy Error 계층은 Softmax의 출력 (y1, y2, y3)와 정답 레이블 (t1, t2, t3)를 받고, 이 데이터들로부터 손실 L을 출력한다.

 

 

[그림 23]에서 주목할 것은 역전파의 결과이다. Softmax 계층의 역전파는 (y1-t1, y2-t2, y3-t3)라는 깔끔한 결과를 내놓고 있다.

 

(y1, y2, y3)는 Softmax 계층의 출력이고 (t1, t2, t3)는 정답 레이블이므로 (y1-t1, y2-t2, y3-t3)는 Softmax 계층의 출력과 정답 레이블의 차분인 것이죠.

 

신경망의 역전파에서는 이 차이인 오차가 앞 계층에 전해지는 것이다. 이는 신경망 학습의 중요한 성질이다.

 

 

신경망 학습의 목적은 신경망의 출력(Softmax의 출력)이 정답 레이블과 가까워지도록 가중치 매개변수의 값을 조정하는 것이었다.

 

그래서 신경망의 출력과 정답 레이블의 오차를 효율적으로 앞 계층에 전달해야 한다.

 

앞의  (y1-t1, y2-t2, y3-t3)라는 결과는 바로 Softmax 계층의 출력과 정답 레이블의 차이로, 신경망의 현재 출력과 정답 레이블의 오차를 있는 그래도 드러내는 것이다.

 

 

구현해보자.

# 다중 클래스 분류의 출력층 활성화함수 소프트맥스(2)
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y
    
# label이 one hot encoding 일때
def cross_entropy_error(y, t):
    if y.ndim == 1:    # 데이터 []로 한 개면 [[]]로 바꿔줌 
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
        
    batch_size = y.shape[0]
    return -np.sum(t * np.log(y + 1e-7)) / batch_size
    
class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None # 손실
        self.y = None # softmax의 출력
        self.t = None # 정답 레이블 (원-핫 벡터)
        
    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss
    
    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size
        
        return dx

==> 역전파 때는 전파하는 값을 배치의 수 (batch_size)로 나눠서 데이터 1개당 오차를 앞 계층으로 전파하는 점에 주의하자.

 

 

 

 

 

오차역전파법 구하기

---

지금까지 구현한 계층을 조합해서 신경망을 구축해보겠다.

 

2층 신경망을 TwoLayerNet 클래스로 구현하겠다.

import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict

class TwoLayerNet:
    
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        
        # 가중치 초기화
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)
        
        # 계층 생성
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
        
        self.lastLayer = SoftmaxWithLoss()
        
    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
            
        return x
    
    # x: 입력 데이터, t: 정답 레이블
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1: 
            t = np.argmax(t, axis=1)
            
        accuracy = np.sum(y == t) / float(x.shape[0])
            
        return accuracy
    
    # x: 입력 데이터, t: 정답 레이블
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        
        return grads
    
    def gradient(self, x, t):
        # 순전파
        self.loss(x, t)
        
        # 역전파
        dout = 1
        dout = self.lastLayer.backward(dout)
        
        layers = list(self.layers.values())
        layers.reverse()
        
        for layer in layers:
            dout = layer.backward(dout)
            
        # 결과 저장
        grads = {}
        grads['W1'] = self.layers['Affine1'].dW
        grads['b1'] = self.layers['Affine1'].db
        grads['W2'] = self.layers['Affine2'].dW
        grads['b2'] = self.layers['Affine2'].db
        
        return grads

 

여기서는 특히 신경망의 계층을 OrderedDict에 보관하는 점이 중요하다.

 

OrderedDict은 순서가 있는 딕셔너리이다.

 

그래서 순전파 때는 추가한 순서대로 각 계층의 forward() 메서드를 호출하기만 하면 처리가 완료된다.

 

마찬가지로 역전파 때는 계층을 반대 순서로 호출하기만 하면 된다.

 

Affine 계층과 ReLU 계층이 각자의 내부에서 순전파와 역전파를 제대로 처리하고 있으므로, 여기서는 계층을 올바른 순서로 연결한 다음 순서에 맞게 호출해주면 된다.

 

 

 

 

 

오차역전파법으로 구한 기울기 검증하기

---

이전 포스팅에서 오차역전파 대신 사용했던 수치 미분은 오차역전파법을 정확히 구현했는지 확인하기 위해 필요하다.

 

두 방식으로 구한 기울기가 일치함을 확인하는 작업을 기울기 확인(gradient check)이라고 한다.

 

기울기 확인은 다음과 같이 구현한다.

import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

x_batch = x_train[:3]
t_batch = t_train[:3]

grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backprop = network.gradient(x_batch, t_batch)

# 각 가중치 차이의 절대값을 구한 후, 그 절댓값들의 평균을 낸다
for key in grad_numerical.keys():
    diff = np.average(np.abs(grad_backprop[key] - grad_numerical[key]))
    print(key + ":" + str(diff))

Out:   
W1:3.9268309090947133e-10
b1:2.318405479569802e-09
W2:6.199344099721318e-09
b2:1.3990993973783672e-07

 

이 결과는 수치 미분과 오차역전파법으로 구한 기울기의 차이가 매우 작다고 말한다.

 

이로써 오차역전파법으로 구한 기울기도 올바름이 드러나면서 실수 없이 구현했다는 믿음이 커지는 것이다.

 

 

 

 

 

오차역전파법을 사용한 학습 구현

---

오차역전파법을 사용한 신경망 학습을 구현하며 마무리하겠다.

 

import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000  # 반복 횟수
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 오차역전파법으로 기울기를 구한다
    grad = network.gradient(x_batch, t_batch)
    
    # 갱신
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
        
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print(train_acc, test_acc)

Out:
0.13213333333333332 0.1321
0.9052833333333333 0.9071
0.9215333333333333 0.9239
0.9345166666666667 0.9321
0.9447333333333333 0.9424
0.9525333333333333 0.9507
0.9572666666666667 0.955
0.9611 0.9595
0.9657666666666667 0.962
0.9681166666666666 0.9647
0.97045 0.9655
0.9726166666666667 0.9654
0.9739 0.9681
0.97605 0.9687
0.9776166666666667 0.9696
0.9778666666666667 0.969
0.9796666666666667 0.9708