[ICLR 2022] Learning Strides in Convolutional Neural Networks - 아는 만큼 읽기

DiffStride: Learning Strides in Convolutional Neural Networks

 

 

Intro

글로벌 최고 권위 머신러닝 학회 'ICLR(International Conference on Learning Representations) 2022'에서

Outstanding Paper Award를 수상한 7개의 논문 중 가장 흥미를 끌었던 논문은 CNN 관련 논문이었다.

 

"Learning Strides in Convolutional Neural Networks"

Learning Strides in Convolutional Neural Networks

CNN은 NLP 입문자들도 초입에 접하는 모델이다. 기본적인 성능이 좋아 여러 가지 데이터에 자주 사용되는 모델이지만, Hyper-parameter를 어떻게 설정하냐에 따라 성능이 크게 변하는 모델이기도 하다. 그만큼 Hyper-parameter값 조절은 CNN 딥러닝 모델을 만드는 모든 이들의 큰 숙제이다.

 

위 논문은 CNN을 이용한다면 누구나 직면하는 고민중 하나인 Stride 값을 미분가능한 요소로 분해한 후, Gradient Decent와 같은 학습법으로 풀어버리는 "DiffStride" 메커니즘를 제안했다. 디테일한 방법론을 설명하기 전에 필자와 같은 NLP 입문자들을 위해 CNN부터 언급하며 시작하겠다.

 

 

CNN

CNN(Convolutional Neural Network)은 크게 Convolution Layer와 Pooling Layer로 구성된다.

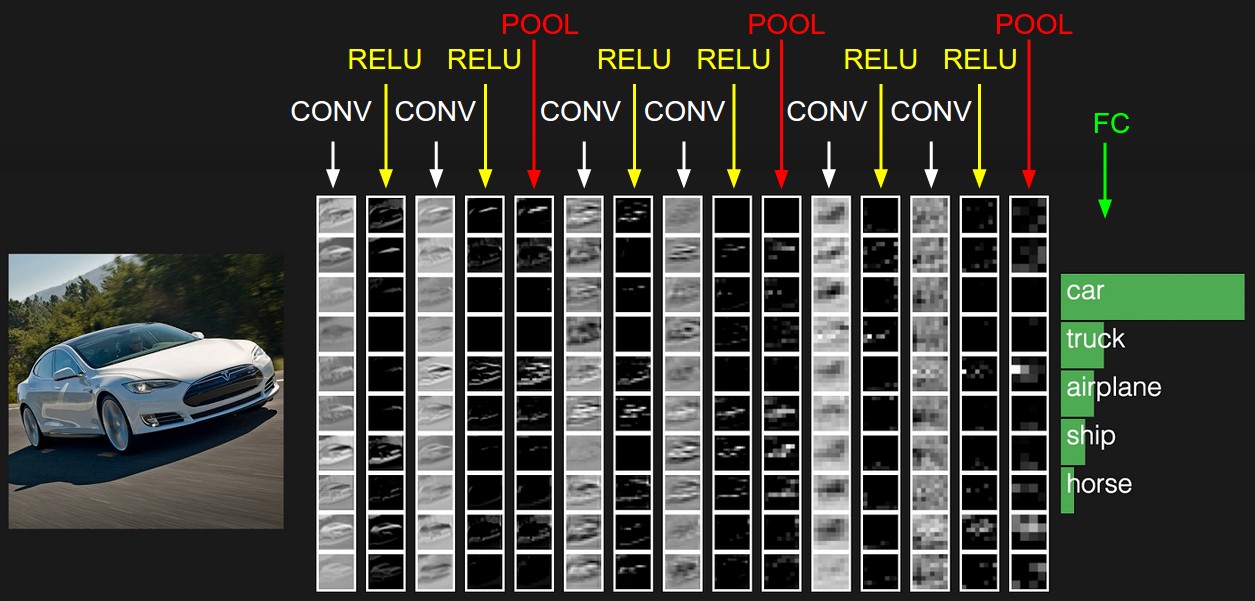
CNN 구조

위 그림에서 CONV는 Convolution 연산을 의미하고, ReLU는 그 연산 결과가 지나가는 활성화 함수이다. CONV + ReLU를 Convolution Layer이라 칭하며, 그 후 지라는 POOL이 바로 Pooling Layer이다. 두 개의 Layer를 좀 더 자세히 학습해보자.

 

# Convolution Layer?

Convolution Layer는 Convolution 연산을 통해 Input(보통 이미지)의 특징을 추출하는 역할을 한다.

Convolution 연산이란 커널(kernel) 또는 필터(filter) 라는 n×m 크기의 행렬로 높이(height)×너비(width) 크기의 이미지를 처음부터 끝까지 겹치며 훑으면서 n×m 크기의 겹쳐지는 부분의 각 이미지와 커널의 원소의 값을 곱해서 모두 더한 값을 출력으로 하는 것을 말한다.

글로 읽으면 어렵다는 것을 필자도 잘 알고있기 때문에, 아래 연산 과정 애니메이션과 함께 이해하는 것을 추천한다.

파란색 사각형 부분이 Input 데이터, 파란색 사각형에서 그림자가 생기는 부분이 Kernel, 그리고 초록색 사각형 부분이 Output인 Feature Map(특성맵)이다.

No Padding, Stride=1	Padding, Stride=1
No Padding, Stride=2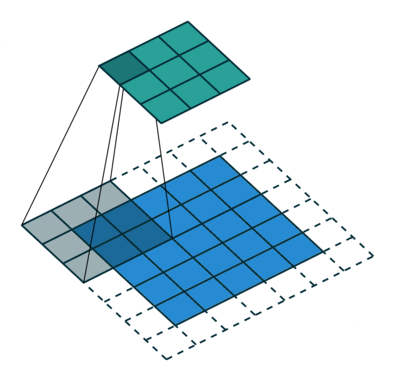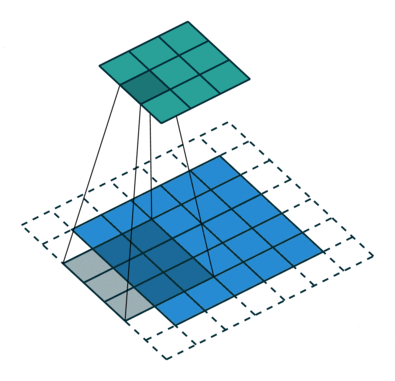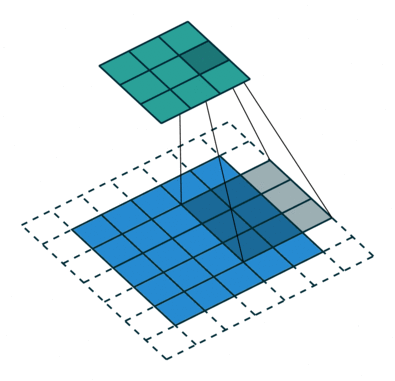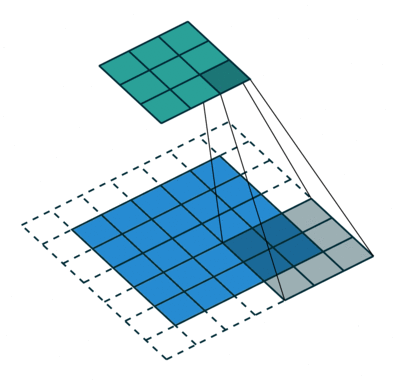	Padding, Stride=2

 

# Padding, Stride?

각 애니메이션 각각 달려있는 부연 설명을 보면 Padding, Stride라는 용어가 적혀져 있는데, 처음 듣는 이를 위해 간단하게 설명해보겠다.

먼저 점선의 유무에 따라 Padding 유무가 달라지는 것을 보면 알 수 있듯, Padding이란 Convolution 연산을 하기 전에 Input의 가장자리에 지정된 개수의 폭 만큼 행과 열을 추가해주는 것을 말한다. 쉽게 말해 지정된 개수의 폭만큼 테두리를 추가하는 것이다. 주로 값을 0으로 채우는 제로 패딩(zero padding)이 사용된다.

오늘 읽을 논문의 가장 중요한 용어인 Stride는 Kernel의 이동 범위를 의미한다. 애니메이션 첫 줄의 Stride=1인 연산은 그림자 Kernel이 한 칸씩 이동하고 있고 아래 줄의 Stride=2는 Kernel이 두 칸씩 점프하며 넘어가는 것을 보면 쉽게 이해가 갈 것이다.

 

# Pooling Layer?

Pooling Layer에서는 Convolution Layer에서 추출된 Feature Map(특성맵)을 Downsampling하여 크기를 줄이는 연산이 이루어진다. 일반적으로 Max Pooling(최대 풀링)과 Average Pooling(평균 풀링)이 사용된다.

최대 풀링 (Max Pooling)

Pooling 연산에서도 Convolution 연산과 마찬가지로 Kernel과 Stride의 개념을 가진다. 위의 그림은 Stride가 2일 때, 2 × 2 크기 Kernel로 Max Pooling을 했을 때 Feature Map이 절반의 크기로 Downsampling되는 것을 보여준다. Max Pooling은 Kernel과 겹치는 영역 안에서 최대값을 추출하는 방식이다.

다른 풀링 기법인 Average Pooling은 이름에서부터 알 수 있듯 최대값이 아니라 평균값을 추출하는 연산이다. 풀링 연산은 Kernel과 Stride 개념이 존재한다는 점에서 Convolution 연산과 유사하지만, 학습해야 할 가중치가 없으며 연산 후에 채널* 수가 변하지 않는다는 차이를 지닌다.

 

* 채널 : 기계는 글자나 이미지보다 숫자. 다시 말해, 텐서를 더 잘 처리한다. 이미지는 (높이, 너비, 채널)이라는 3차원 텐서이다. 여기서 높이는 이미지의 세로 방향 픽셀 수, 너비는 이미지의 가로 방향 픽셀 수, 채널은 색 성분을 의미한다. 흑백 이미지는 채널 수가 1이며, 각 픽셀은 0부터 255 사이의 값을 진다. 우리가 통상적으로 접하게 되는 컬러 이미지는 적색(Red), 녹색(Green), 청색(Blue) 채널 수가 3개이다.

 

# 읽어도 모르겠다면?

참고로 더 원초적인 CNN관련 설명을 보고 싶다면, 필자가 작성해둔 CNN 기초를 보고와도 좋다!

https://dokylee.tistory.com/50

[NLP] 합성곱 신경망 CNN : 합성곱 연산, 배치 처리, 풀링 계층

 

 

DiffStride

CNN의 요소들을 간단히 학습해보았으니, 오늘의 메인 주제인 DiffStride 메커니즘으로 넘어가보겠다.

논문을 처음부터 쭉 읽어본 입장에서 DiffStride는 한 마디로 이렇다.

DiffStride란 학습 가능한 Stride 변수를 지닌 Pooling Layer이다.

 

학습 가능한 Stride라니, 위의 CNN 설명과 상반된 문장이다. 분명 Pooling Layer는 학습 파라미터가 없는 층이라 언급했었는데, 이 논문은 학습 가능한 Stride 변수를 가진 Pooling Layer 메커니즘을 제안했다.

 

CNN은 위에서 언급했듯 Convolution Layer, Pooling Layer 모두 Downsampling되는 특징을 지니고 있다. 이와 같은 Layer는 전체적인 모델의 계산 복잡도를 낮춰주지만, 동시에 모델은 원본 Input의 특성을 보존해야 하므로 Shift-invariance(=쉽게 말해 x값이 이동해도 y값이 동일하게 나오는 것)을 만족해야 한다. 이러한 Layer의 가장 중요한 Hyper-parameter는 Stride이다. 그러나 Stride는 미분 불가능한 Constant 값이기 때문에, 최적의 Stride 값을 찾기 위해서는 Cross-validation이나 Architecture search* 같은 별개의 최적화 작업이 필요하다. 또한 최적화 작업을 한다고 해도 Downsampling Layer 수가 증가함에 따라 Search Space가 지수적으로 증가하기 때문에 거의 불가능에 가까운 작업이 된다. 이러한 비용을 감소시키기 위해, DiffStride는 cropping mask의 크기를 Fourier Transform*을 이용해 미분 가능하게 하여 학습한 후 resizing을 반복하며 최적의 크기를 찾는다. 이 메커니즘은 임의의 Stride 값으로 시작했음에도 CIFAR10, CIFAR100, ImageNet 이미지 데이터셋에서 좋은 성능을 기록했으며, 모델 구조의 계산 복잡도를 조절할 수 있는 Regularization 기능 또한 가능하여 연산 및 메모리 사용량을 최소화하게 했다.

 

* Architecture Search :  주어진 Task에 가장 최적인 네트워크 구조를 자동으로 탐색하는 방법론을 연구하는 분야

* Fourier Transform (푸리에 변환) : 푸리에 변환은 임의의 입력 신호를 다양한 주파수를 갖는 주기함수들의 합으로 분해하여 표현하는 것이다. 푸리에 변환에서 사용하는 주기함수는 sin, cos 삼각함수이며, 고주파부터 저주파까지 다양한 주파수 대역의 sin, cos 함수들로 원본 신호를 분해한다.

 

 

Pooling Layer는 크게 아래 두 가지 작업으로 나뉜다.

1. Input의 local 통계치를 노이즈 없이 밀도있게 표현 (e.g. Max Pooling, Average Pooling)
2. 정수값 Stride를 통해 local 통계치를 Sub-sampling

지금까지 대부분의 연구는 1번의 알고리즘을 고도화 하는데 치중되어 있었으나, 중요한 것은 1번이 아무리 좋아진다고 해도 2번의 정수값 Stride가 Feature Map의 resolution(해상도)를 급격하게 감소시켜 원본 정보를 보존하는데 한계를 지니게 한다는 점이었다.

2015년 Rippel*또한 이 논문처럼 Fourier 변환을 통한 저주파 대역을 강조한 후 Fractional Stride를 만들어 Input을 cropping하는 Spectral Pooling 기법을 제안했으나, DiffStride는 Hyper-paremeter로써의 고정된 box 크기로 cropping하는 것이 아니라 Backpropagation을 통해 cropping box를 학습하여 모델에 적용한다는 점이 그와 달랐다.

 

* Oren Rippel, Jasper Snoek, and Ryan P Adams. Spectral representations for convolutional neural

networks. In Proceedings of the 28th International Conference on Neural Information Processing

Systems-Volume 2, pp. 2449–2457, 2015. 2, 3, 6

https://proceedings.neurips.cc/paper/2015/file/536a76f94cf7535158f66cfbd4b113b6-Paper.pdf

 

 

DiffStride이 어떠한 아이디어인지 알았으니, 아래 그림을 보며 작동원리를 간단히 살펴보자.

DiffStride Mechanism

위 과정은 single-channel image(흑백사진)에 대한 DiffStride의 Forward, Backward 과정이다. 

아래 W라고 쓰여진 box가 바로 Input과 Stride, 그리고 R(smoothness factor)로 매개된 학습되는 box이다. 이 box 관련 값은 DFT(Discrete Fourier Transform)*를 통해 계산된다.

 

계산된 W는 아래 두 가지로 사용된다.

1. Input을 저주파 통과 필터(Low-pass Filter)를 수행하는 푸리에 변환으로 표현한다.  -> element-wise product 사용됨
2. mask가 0인 곳의 푸리에 계수(coefficient)를 crop한다.

첫 번째 과정은 Stride인 S에 대해 미분 가능하지만, 두 번째 cropping 연산은 불가능하다. 따라서 cropping 전에 Stop Gradient operator*라는 기능을 mask에 적용한 후 사용했다고 한다. 이 방법을 통해 Stride가 미분 불가능한 cropping을 통하게 하지 않고, 미분 가능한 저주파 통과 필터 연산을 통하게 하여 Gradient를 통한 학습이 가능해진다고 한다. 마지막으로 DFT로 구해졌던 Stride box 값과 반대로 cropped된 tensor를 inverse DFT 연산을 통해 spatial domain으로 되돌린다. 이 모든 스텝들이 아래 수식으로 요약된다.

DiffStride Algorithm

 

* DFT(Discrete Fourier Transform) : 컴퓨터는 이산적인 값만 처리가 가능하다. 연속시간신호는 시간축(x축)에서 연속적이기 때문에 샘플링을 하여 이산시간 신호를 만들어야한다. 이와 같은 논리로, 이산시간신호에 대한 주파수변환인 DTFT(Discrete Time Fourier Transform)결과를 확인하면, 변환을 통해 x축이 주파수가 되고 y축은 그 주파수성분에 해당하는 값이 나오게 되는데, 이산시간 비주기신호에 대하여 DTFT를 수행한 결과는 연속주기의 형태로 나오게 된다. 그러므로 DTFT결과는 주파수축에서 연속적이기 때문에 컴퓨터에서 처리할 수 없다. 결론적으로는 이산시간신호를 주파수변환하는 DTFT는 컴퓨터에서 쓸 수 없다. 그래서 연속적으로 존재하는 주파수를 쪼개서 이산적으로 만들어야할 필요가 생겼다. 대체할 수 있는 방법으로 나온 것이 DFT이고 이는 DTFT의 주파수샘플링 된 형태가 된다. 정리하면, 시간축에서의 샘플링처럼 DFT를 통해서 주파수축에서 샘플링하여 컴퓨터가 푸리에 변환을 처리할 수 있게 하는 것이다.

 

* Stop Gradient operator - Yoshua Bengio, Nicholas L´eonard, and Aaron Courville. Estimating or propagating gradients

through stochastic neurons for conditional computation. arXiv preprint arXiv:1308.3432, 2013.

3, 4

https://arxiv.org/pdf/1308.3432.pdf

 

Experiment Results

Image Classification 부분에서 성능차를 보면, DiffStride는 초기 Stride 값에 영향 받지 않고 좋은 성능을 유지했다. 그외 비교군들은 초기 Stride값이 좋지 않으면 성능이 눈에 보이게 떨어졌다. 특히 CIFAR100에서 Baseline인 Strided Convolution를 보면 66.8%에서 48.2%까지 정확도가 떨어지는 모습을 보였다. 모델은 ResNet을 사용했다고 한다.

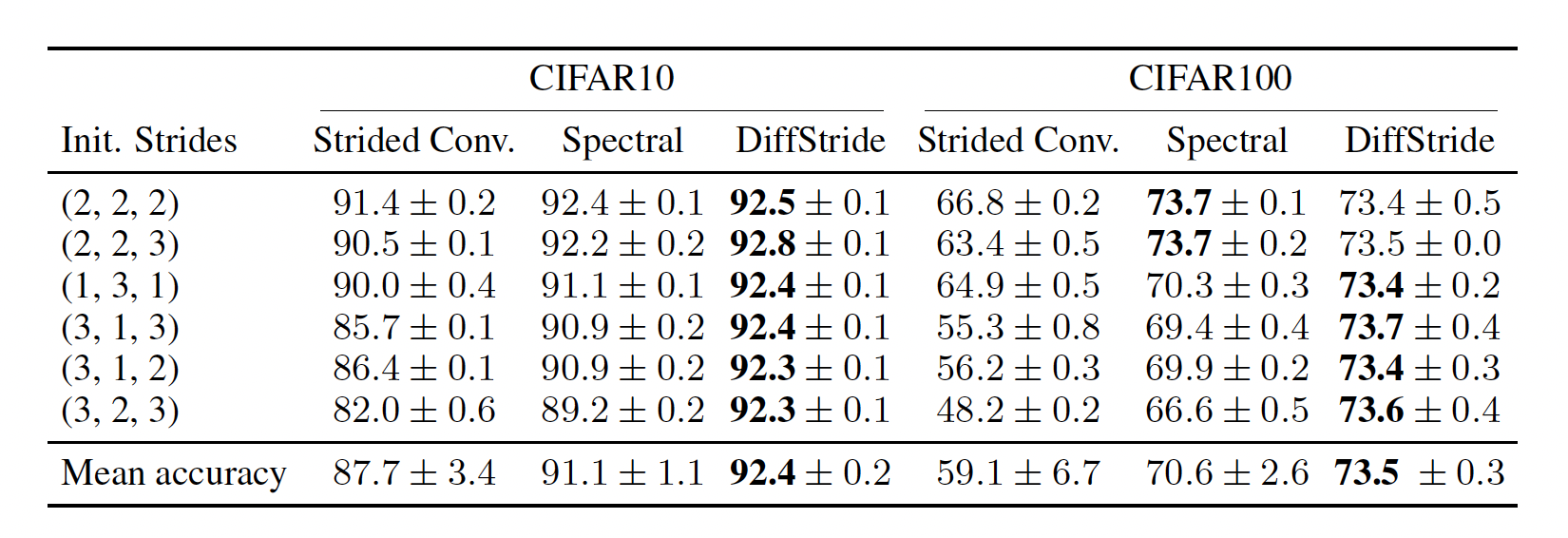
CIFAR10, CIFAR100 데이터셋 Accuracy 비교표

 

 

Conclusion

결론적으로 정리해서 DiffStride는 기존의 Pooling Layer보다 뛰어난 성능으로 풀링 연산을 대체한다고 볼 수 있겠다.

Hyper-parameter로써의 Stride 값을 골치 아프게 고민할 필요없이 임의의 값으로 시작 가능하며, 계산 복잡도를 줄여준다는 특성 때문에 연산 및 메모리 측면에서도 우수했다. 더불어 현재 DiffStride는 Github에 배포되어 있고, 웹 프레임워크 Gin을 통해 parameter customizing까지 가능하여 사용성도 좋다.

요리조리 둘러보아도 DiffStride Layer는 성능 고도화를 위한 좋은 선택지로 보이니, 향후 모델 구조 설계를 할때 고려해볼만 하다고 느낀다.

 

Posting Reference

1. https://wikidocs.net/64066

1) 합성곱 신경망(Convolution Neural Network)

2. https://github.com/vdumoulin/conv_arithmetic

GitHub - vdumoulin/conv_arithmetic: A technical report on convolution arithmetic in the context of deep learning

3. https://cs231n.github.io/convolutional-networks/

CS231n Convolutional Neural Networks for Visual Recognition

4. https://ahn1340.github.io/neural%20architecture%20search/2021/04/26/NAS.html

Neural Architecture Search란?

5. https://lv99.tistory.com/35

AutoML의 대표작: 신경망 아키텍쳐 탐색(Neural Architecture Search; NAS)

6. https://sanghyu.tistory.com/23

DFT(Discrete Fourier Transform)와 Circular Convolution